Wheeled Robots
~ 1.5 cm to a side
temperature sensor & two motors
travels 1 inch in 3 seconds
untethered !!
docsity.com
Prepare for your exams
Study with the several resources on Docsity
Earn points to download
Earn points by helping other students or get them with a premium plan
Guidelines and tips
Prepare for your exams
Study with the several resources on Docsity
Earn points to download
Earn points by helping other students or get them with a premium plan
Community
Ask the community
Ask the community for help and clear up your study doubts
University Rankings
Discover the best universities in your country according to Docsity users
Free resources
Our save-the-student-ebooks!
Download our free guides on studying techniques, anxiety management strategies, and thesis advice from Docsity tutors
Kinematics of Differential and Synchro Drives: Forward and Inverse Kinematics, Slides of Robotics
An in-depth analysis of the kinematics of differential and synchro drives, focusing on forward and inverse kinematics. It covers topics such as system measurements, determining the robot's velocity and position, the instantaneous center of curvature, and solving equations for desired velocities. The document also discusses various wheeled robots and their kinematic challenges.
Typology: Slides
2013/2014
1 / 45
This page cannot be seen from the preview
Don't miss anything!
Related documents
Partial preview of the text
Download Kinematics of Differential and Synchro Drives: Forward and Inverse Kinematics and more Slides Robotics in PDF only on Docsity!
Wheeled Robots
~ 1.5 cm to a side
temperature sensor & two motors
travels 1 inch in 3 seconds
untethered !!
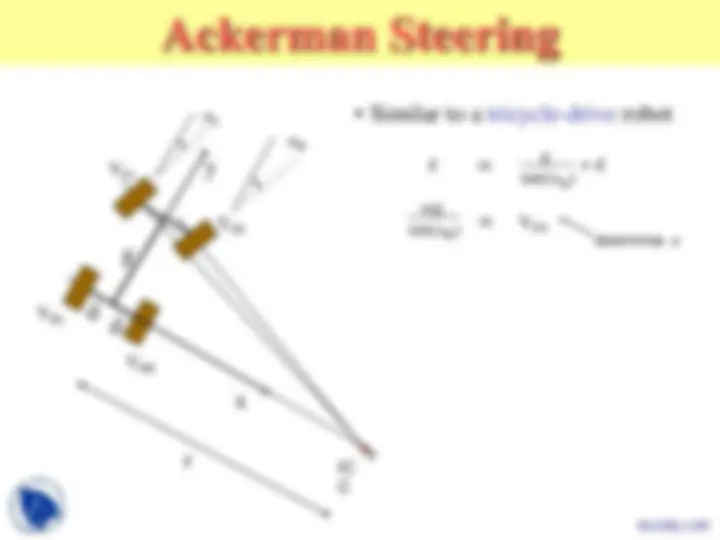
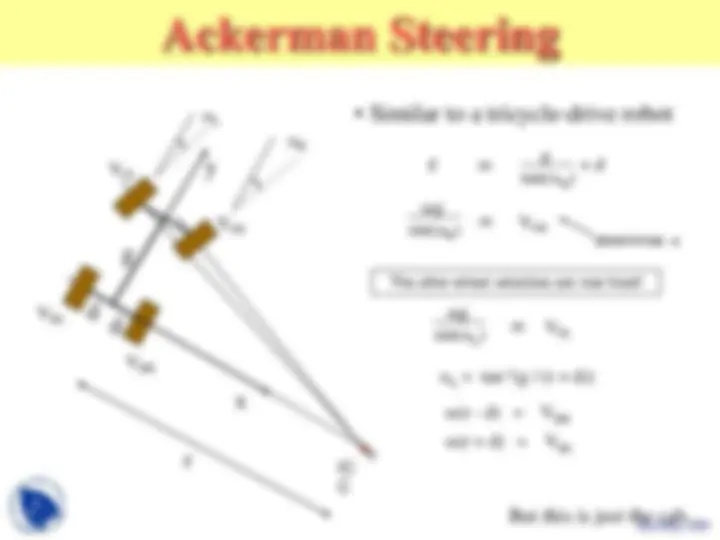
Other mini machines
Pocketbot
Khepera
“Cricket”
radio unit linear vision gripper video 55mm dia. base
- Specify system measurements
- Determine the point (the radius) around which the robot is turning.
- Determine the speed at which the robot is turning to obtain the robot velocity.
- Integrate to find position. Kinematics of Differential drive
Differential Drive is the most
common kinematic choice
All of the miniature robots…
Pioneer, Rug warrior
- difference in wheels’ speeds
determines its turning angle
VR
VL
Questions (forward kinematics)
Given the wheel’s velocities or positions,
what is the robot’s velocity/position?
Are there any inherent system constraints?
- Specify system measurements VR
VL
(assume a wheel radius of 1)
x
y
q 2d
- consider possible coordinate systems Kinematics of Differential drive
- Specify system measurements VR
VL
(assume a wheel radius of 1)
x
y
q 2d
- consider possible coordinate systems
- Determine the point (the radius) around which the robot is turning. ICC “instantaneous center of curvature”
- to minimize wheel slippage, this point (the ICC ) must lie at the intersection of the wheels’ axles
- each wheel must be traveling at the same angular velocity Kinematics of Differential drive – angular velocity
= angular velocity docsity.com
- Specify system measurements VR
VL
(assume a wheel radius of 1)
x
y
q 2d
- consider possible coordinate systems
- Determine the point (the radius) around which the robot is turning. ICC “instantaneous center of curvature”
- to minimize wheel slippage, this point (the ICC ) must lie at the intersection of the wheels’ axles
- each wheel must be traveling at the same angular velocity around the ICC w Kinematics of Differential drive
- Specify system measurements VR
VL
(assume a wheel radius of 1) 2d
- consider possible coordinate systems
- Determine the point (the radius) around which the robot is turning. ICC
- each wheel must be traveling at the same angular velocity around the ICC R robot’s turning radius
- Determine the robot’s speed around the ICC and then linear velocity w w(R+d) = VL w(R-d) = VR Thus, w = ( VR - VL ) / 2d R = 2d ( VR + VL ) / ( VR - VL )
x
y
Kinematics of Differential drive ICC “instantaneous center of curvature”
- Specify system measurements VR
VL
2d
- consider possible coordinate systems
- Determine the point (the radius) around which the robot is turning. ICC
- each wheel must be traveling at the same angular velocity around the ICC R robot’s turning radius
- Determine the robot’s speed around the ICC and then linear velocity w w(R+d) = VL w(R-d) = VR Thus, w = ( VR - VL ) / 2d R = 2d ( VR + VL ) / ( VR - VL )
x
y
So, the robot’s velocity is (^) V = wR = ( V R + VL ) / 2 Kinematics of Differential drive – robot’s velocity
- Integrate to obtain position VR
VL
2d ICC R(t) robot’s turning radius w(t) w = ( VR - VL ) / 2d R = 2d ( VR + VL ) / ( VR - VL ) V = wR = ( VR + VL ) / 2 Vx = V(t) cos(q(t)) Vy = V(t) sin(q(t)) with
x
y
x(t) = ∫ V(t) cos(q(t)) dt
y(t) = ∫ V(t) sin(q(t)) dt
q(t) = ∫ w(t) dt
Thus, Kinematics of Differential drive
Velocity Components VR
VL
2d ICC R(t) robot’s turning radius w(t) Thus, w = ( VR - VL ) / 2d R = 2d ( VR + VL ) / ( VR - VL ) What has to happen to change the ICC?^ V^ =^ wR = ( VR + VL ) / 2 Vx = V(t) cos(q(t)) Vy = V(t) sin(q(t))
x(t) = V(t) cos(q(t)) dt
y(t) = V(t) sin(q(t)) dt
q(t) = w(t) dt
with
x
y
Kinematics
Kinematics of Differential drive – velocity components speed
Nomad 200
wheels rotate in tandem and remain parallel
all of the wheels are driven at the same speed
Where is the ICC? Kinematics of Synchro drive – wheels synchronized
Nomad 200
wheels rotate in tandem and remain parallel
all of the wheels are driven at the same speed
x
y
q w Vwheels
V
robot
= V
wheels
w
robot
= w
wheels
x(t) = Vwheels(t) cos(q(t)) dt
y(t) = Vwheels(t) sin(q(t)) dt
q(t) = w(t) dt
position velocity simpler to control, but ... ICC at Kinematics of Synchro drive – velocity and position
Synchro Drive using Lego more difficult to build. this light sensor follows the direction of the wheels, but the RCX is stationary also, four bump sensors and two motor encoders are included But how do we get somewhere? docsity.com
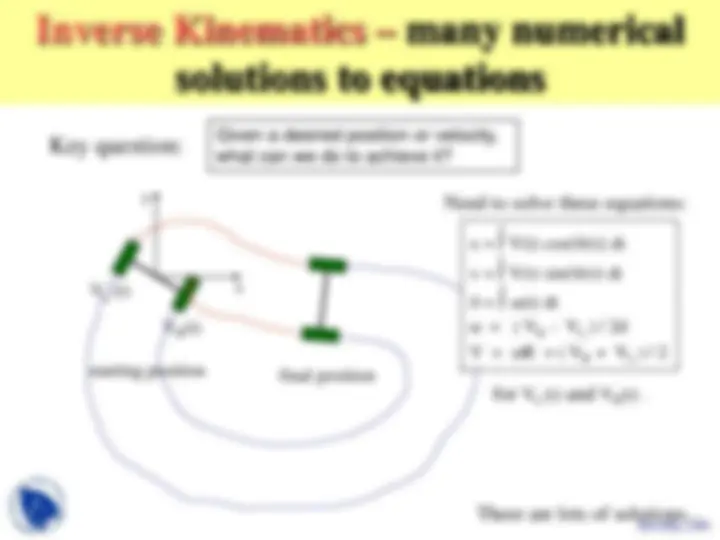
Inverse Kinematics of Differential Drive